К разделу 'Математика' сайта AlgoList.

Домой Оглавление

Нормальное распределение*

* - подробней о способах вычисления нормального распределения можно почитать в посвященной этому статье П.Н.Дубнера

Обозначение N(x|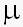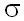mu, sigma)
Область значений
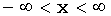Параметры

Параметр положения , математическое ожидание.
Параметр масштаба , стандартное отклонение.
Плотность (функция вероятности)

Математическое ожидание
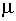Дисперсия
Функция распределения Не выражается в элементарных функциях

  Связь с другими распределениями


Пусть 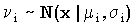, i = 1..K – независимые нормально распределенные случайные величины. Тогда сумма 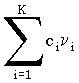подчиняется нормальному распределению с параметрам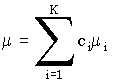и и .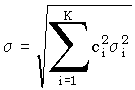

В частности, сумма n независимых одинаково распределенных нормальных случайных величин 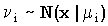, i = 1..n, распределена нормально с средним n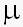mu и стандартным отклонением .

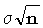Сумма квадратов независимых случайных величин 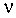i, распределенных одинаково нормально с параметрами 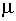=0, 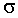=1, подчиняется распределению хи-квадрат с n степенями свободы: .

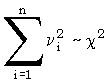Стандартное нормальное распределение является частным случаем гамма-распределения:

,

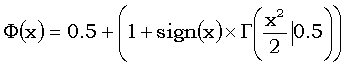где

.

 


  Генерация случайных чисел


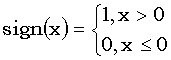Пусть ri – независимы и распределены равномерно на [0,1]. Поскольку математическое ожидание ri равно 1/2, а дисперсия 1/12, то согласно центральной предельной теореме распределение суммы

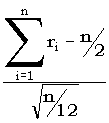
с ростом n стремится к нормальному с параметрами 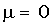, 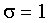. Особенно простая формула получается, если взять n = 12.

Две независимые нормальные случайные величины 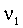и 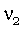можно получить из двух независимых равномерно распределенных на [0,1] случайных величин r1 и r2 с помощью соотношений:

, .


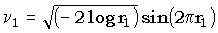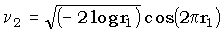  Вычисление функции распределения и ее квантилей


Способам вычисления нормального распределения я посвятил специальный текст, поэтому здесь ограничусь лишь двумя иллюстрациями.

Функция normalDF, позволяющая вычислять с "произвольной" точностью, использует указанную связь с гамма-распределением; чтобы эти коды работали, потребуются файлы loggamma.h и loggamma.cpp (см. Приложение А). Функция же inv_normalDF предназначена для вычисления квантилей нормального распределения с примерно тремя знаками. В ней использован алгоритм Z2 из $3 упомянутого текста про способы вычисления нормального распределения; заодно коды демонстрируют применение правила Горнера при вычислении полинома.

Файл normalDF.h

/****************************************************/
/*                 Нормальное распределение         */
/****************************************************/

#ifndef __NORMAL_H__                    /* To prevent redefinition           */

#define ENTRY   extern
#define LOCAL   static

double normalDF(double x);
/* Вычисляет вероятность того, что случайная величина,
 * подчиняющаяся стандартному нормальному распределению,
 * принимает значение, не превосходящее x.
 */

double inv_normalDF(double level);
/* Вычисляется квантиль уровня level,
 * который, согласно определению, является корнем уравнения
 *		N(x) = level,
 * где N(x) - стандартное нормальное распределение.
 * Решение уклоняется от точного значения не более, чем на 0.00045.
 * Конечно, значение level должно быть заключено между 0 и 1.
 */


#define __NORMAL_H__                    /* Prevents redefinition             */
#endif                                  /* Ends #ifndef __NORMAL_H__         */

Файл normalDF.cpp

/****************************************************/
/*                 Нормальное распределение         */
/****************************************************/
#include "normalDF.h"
#include "gammaDF.h"

ENTRY double
normalDF(double x)
/* Вычисляет вероятность того, что случайная величина,
 * подчиняющаяся стандартному нормальному распределению,
 * принимает значение, не превосходящее x.
 */
{
   double dfg;
   if (x == zero)
      return 0.5;
   dfg = gammaDF(0.5, x * x / 2) / 2;
   return 0.5 + (x > zero ? dfg : -dfg);

}/*normalDF*/

ENTRY double
inv_normalDF(double level)
/* Вычисляется квантиль уровня level,
 * который, согласно определению, является корнем уравнения
 *		N(x) = level,
 * где N(x) - стандартное нормальное распределение.
 * Решение уклоняется от точного значения не более, чем на 0.00045.
 * Конечно, значение level должно быть заключено между 0 и 1.
 */
{
   double q, t;

   assert((level > zero) && (level < one));
   t = level < 0.5 ? level : one - level;
   t = sqrt(-2 * log(t));
   q = t - ((0.010328 * t + 0.802853) * t + 2.515517) /
      (((0.001308 * t + 0.189269) * t + 1.432788) * t + 1);
   return level > 0.5 ? q : -q;
}/*inv_normalDF*/

Дата последней модификации: 25 октября 2000 г.