|
|
В последовательности испытаний
Бернулли с вероятностью успеха p и вероятностью неудачи q=1-p число y неудач до x-го
успеха имеет отрицательное биномиальное распределение.
| Обозначение | Y(y|x,p) – число неудач |
| Область значений | 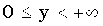 y – целое y – целое
|
| Параметры |
x – число успехов, целое положительное число
p – вероятность успеха, 0 < p < 1 |
| Плотность (функция вероятности) |
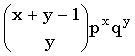
|
| Математическое ожидание | xq/p |
| Дисперсия | xq/p2 |
| Функция распределения |
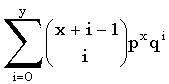
|
В горячо рекомендуемом справочнике М.Абрамовица и И.Стигана ("Справочник по специальным функциям", М: Мир 1979, [26.5.26]) предлагается следующая связь отрицательного биномиального распределения с бета-распределением:
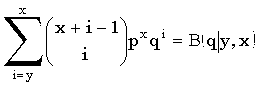 .
.Сумма k
независимых случайных величин 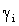 ,
i = 1..k,
распределенных геометрически с параметром p,
подчиняется отрицательному биномиальному распределению с
,
i = 1..k,
распределенных геометрически с параметром p,
подчиняется отрицательному биномиальному распределению с 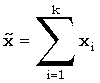 .
.
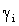 ,
i=1..x: случайная
величина
,
i=1..x: случайная
величина 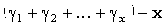 имеет
отрицательное биномиальное распределение.
Случайные величины
имеет
отрицательное биномиальное распределение.
Случайные величины 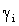 получаются из ri,
равномерно распределенных на [0,1], согласно следующей формуле:
получаются из ri,
равномерно распределенных на [0,1], согласно следующей формуле: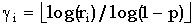 ,
где
,
где 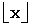 – значение x, округленное
в большую сторону до ближайшего целого числа.
– значение x, округленное
в большую сторону до ближайшего целого числа.
Проще всего, конечно, использовать указанную связь с бета-распределением. Как и для всех дискретных распределений вычисление квантилей объявляется бесполезным. Взамен предлагается найти вероятность успеха, когда известны количества неудач и успехов, а также соответствующее значение функции распределения.
Для вычислений с помощью нижеследующих кодов потребуются файлы betaDF.h, betaDF.cpp (см. раздел о бета-распределении), а также logGamma.h, logGamma.cpp (см. приложение А).
#ifndef __NEGBINOMIAL_H__ /* To prevent redefinition */ #define ENTRY extern #define LOCAL static double negBinomialDF(long k, long n, double p); /* * Для последовательности испытаний Бернулли вычисляется * вероятность того, что n-му успеху предшествуют k * или меньше неудач. * * Все аргументы должны быть положительными, причем 0 < p < 1. */ double rev_negBinomialDF(long k, long n, double y); /* * Ищется значение p, для которого negBinomialDF(k,n,p) = y. * */ #define __NEGBINOMIAL_H__ /* Prevents redefinition */ #endif /* Ends #ifndef __NEGBINOMIAL_H__ */ |
#include <assert.h>
#include <math.h>
#include "betaDF.h"
double negBinomialDF(long k, long n, double p)
/*
* Для последовательности испытаний Бернулли вычисляется вероятность того,
* что n-му успеху предшествуют k или меньше неудач, т.е. сумму
* членов отрицательного биномиального распределения от 0 до k:
*
* k
* -- ( n+j-1 ) n j
* > ( ) p (1-p)
* -- ( j )
* j=0
*
* При вычислении функции распределения ряд не суммируется.
* Используется ее связь с бета-распределением:
*
* y = negBinomialDF(k, n, p) = betaDF(n, k+1, p).
*
* Все аргументы должны быть положительными, причем 0 < p < 1.
*/
{
assert( (n > 0) && ( k >= 0 ) && (p >= 0.0) && (p <= 1.0) );
return BetaDF(n, k+1).value(p);
}/*negBinomialDF*/
double rev_negBinomialDF(long k, long n, double y)
/*
*
* Ищется значение p, для которого negBinomialDF(k,n,p) = y.
*
*/
{
assert( (n > 0) && ( k >= 0 ) && (y >= 0.0) && (y <= 1.0) );
return BetaDF(n, k+1).inv(y);
}/*rev_negBinomialDF*/
|
Дата последней модификации: 25 октября 2000 г.