К разделу 'Математика' сайта AlgoList.

Домой Оглавление

Распределение Коши

Обозначение
Область значений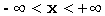
Параметры Параметр расположения a, медиана,
параметр масштаба b > 0.
Плотность (функция вероятности)
Математическое ожидание Не существует
Дисперсия Не существует
Функция распределения

 
  Связь с другими распределениями


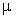Отношение двух независимых одинаково распределенных нормальных случайных величин y1, y2 с средним =0 и стандартным отклонением 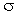=1 подчиняется распределению Коши с параметрами a=0, b=1.

Сумма n независимых случайных величин 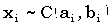, подчиняется распределению Коши с параметрами, равными суммам соответствующих параметров слагаемых:

.
  Генерация случайных чисел


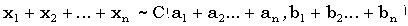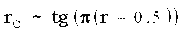Используя стандартный метод перехода от равномерного распределения, получаем формулу: , где r – равномерно распределенное случайное число, а rC подчиняется распределению Коши.
  Вычисление функции распределения и ее квантилей


Не представляет никаких трудностей: используются лишь функции, входящие в стандартные библиотеки (как в Си), либо в сам язык (как в Паскале).

Для совсем ленивых все-таки привожу коды. Помните все же, что использованные стандартные функции работают с ограниченной точностью!

Файл cauchy.h

#ifndef __CAUCHY_H__		/* To prevent redefinition	*/

#define ENTRY   extern
#define	LOCAL	static

ENTRY double cauchyDF(double x, double a, double b);
ENTRY double inv_cauchyDF(double q, double a, double b);

#define __CAUCHY_H__		/* Prevents redefinition	*/
#endif				/* Ends #ifndef__CAUCHY_H__	*/

Файл cauchy.cpp

#include <assert.h>
#include <math.h>

const double pi=3.1415926;
const double half=0.5;

double cauchyDF(double x, double a, double b)
{
   assert(b > 0);
   return half+atan((x-a)/b)/pi;
}

double inv_cauchyDF(double q, double a, double b)
{
   assert((b > 0) && (q > 0) && (q < 1));
   return a+b*tan(pi*(q-half));
}

#ifdef TEST

#include <iostream.h>

void main(void)
{
   double a, b;

   while (1) {
      cout << "\n\n\rEnter a: ";
      cin >> a;
      if (a <= 0)
	 break;
      do {
         cout << "Enter b: ";
         cin >> b;
      } while (b <= 0);

      for(double x=-8; x < 8; x += 0.1)
      {
         double y=cauchyDF(x, a, b);
         cout << "x=" << x << "\tcauchy=" << y;
         double z=inv_cauchyDF(y, a, b);
         cout << "\ti_cauchy=" << z << endl;
      }
   }
}

#endif

Дата последней модификации: 25 октября 2000 г.